Corioliseffect
het Corioliseffect (Bron: http://www.coastalpractice.net)
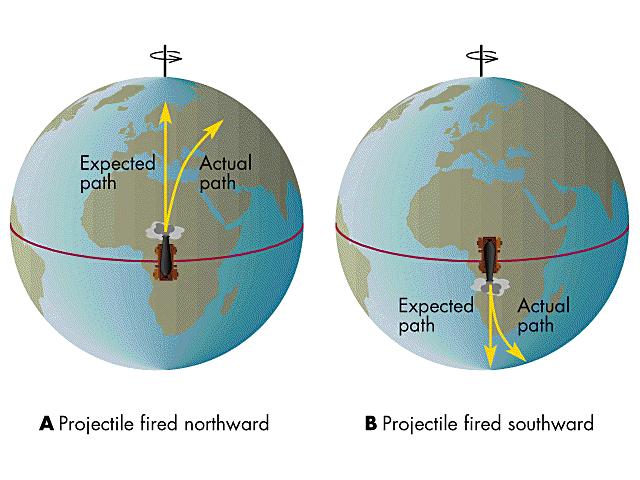
De luchtcirculatie staat onder invloed van de rotatie van de aarde (rond haar as draaien). Dat we dit weten hebben we te danken aan een fanatieke biljarter en natuurkundige Gustave-Gaspard Coriolis. Bij bestudeerde als eerste de draaibeweging van biljartballen. Hij ontdekte dat voorwerpen die in een rechte baan gaan in het noorderlijk halfrond naar rechts afbuigen en in het zuidelijk halfrond naar links afbuigen, ten opzichte van hun bewegingsrichting.
Hoe snel dit gaat, hangt af van de plaats op aarde. De aarde draait om haar eigen as met een hoeksnelheid van ongeveer één omwenteling per dag. Elk punt op aarde zal in net geen 24 uur éénmaal rond die as roteren. De absolute snelheid waarmee dit gebeurt, hangt sterk af van de breedteligging op aarde. Hoe dichter bij de evenaar, hoe groter de snelheid zal zijn; hoe meer richting de polen hoe lager deze snelheid. Je kunt dit makkelijk begrijpen door middel van een experiment. Ga met enkele vrienden hand in hand op een rij staan naast een paal. De persoon dichtst bij de paal houdt deze vast. Maak nu vervolgens een cirkelbeweging rond de paal. De persoon die er het dichtst bij staat, zal al wandelend het tempo kunnen volgen. De persoon die er het verst van af staat, zal zich de ziel uit het lijf moeten lopen om in een zelfde tijd volledig rond de paal te raken. Hij loopt immers in een grotere cirkel. Hiermee is dus duidelijk dat hoe groter de afstand tot de draaias is, hoe groter de snelheid moet zijn om een omwenteling te maken. Zo is op aarde de afstand tot de draaias het grootst ter hoogte van de evenaar, daar zal de snelheid het grootst zijn. Hoe meer men richting de polen trekt, hoe kleiner de afstand tot de as wordt en hoe lager de snelheid zal zijn. Iemand die zich aan de evenaar bevindt, zal aan een grotere snelheid bewegen dan iemand die zich aan de polen bevindt. Het is dit snelheidsverschil dat het zogenaamde ‘Corioliseffect’ veroorzaakt. De richting van de snelheid is in wijzerzin wanneer men de Noordpool van de aarde als bovenaanzicht neemt, tegenwijzerzin wanneer men de Zuidpool als bovenaanzicht neemt.
Een voorbeeld uit de luchtvaart illustreert het corioliseffect. Stel dat we een vliegtuig van Nigeria (gelegen aan de evenaar) naar Zweden laten vliegen. Dit is een tocht van 6 uur in het noorderlijk halfrond. De snelheid van de aarde aan de evenaar bedraagt ongeveer 1600 km/uur. Ter hoogte van Zweden, gelegen op 60° noorderbreedte, bedraagt deze snelheid slechts 800 km/uur. De afstand tot de aardas bedraagt daar immers slechts 3050 km (t.o.v. 6300 km aan de evenaar). Doordat het vliegtuig opstijgt aan de evenaar zal zijn oorspronkelijke snelheid 800 km/uur groter zijn dan de uiteindelijke snelheid ter hoogte van Zweden. Indien er geen correctie zou doorgevoerd worden, zou het vliegtuig dan ook niet In Zweden aankomen, maar 800 km/uur x 6 uur = 4800 km ten oosten van Zweden: een belangrijke afwijking naar rechts ten opzichte van de bewegingsrichting.
Voor de omgekeerde vliegbeweging, van Zweden naar Nigeria, is het omgekeerde waar. De snelheid in Zweden is immers lager dan deze in Nigeria. hierdoor zal een afwijking bestaan van 4800 km naar het westen van Nigeria. Bekijk je deze afwijking ten opzichte van de bewegingsrichting, dan zie je weer een afwijking naar rechts. Op het Zuidelijk halfrond is het principe net hetzelfde, maar hier wordt steeds een afwijking naar links verwacht ten opzichte van de bewegingsrichting.
Het is van belang te benadrukken dat het corioliseffect ontstaat door de verschillende snelheden waarmee een punt op de aarde omheen de draaias beweegt. Het is een hardnekkige misvatting te denken dat een opstijgend voorwerp als het ware los komt van de aarde waarbij de aarde onder het voorwerp blijft verder roteren. Als je springt op een bus die rijdt aan een hoge snelheid, dan zal je op exact dezelfde plaats neerkomen van waar je vertrokken bent. Ten opzichte van de baan heb jij immers dezelfde snelheid als de bus. Zo ook zal een helicopter die stijgt tot hoog boven de aarde bij landing op dezelfde plaats terug neer komen. Zolang de helikopter immers op dezelfde breedtegraad blijft, zal zijn rotationele snelheid gelijk zijn aan deze van de aarde en zal er tussen helikopter en landingsplaats geen snelheidsverschil bestaan.
Het corioliseffect is uiteraard niet alleen van toepassing op vliegtuigen, bommen en andere projectielen, maar op elke bewegende massa dus ook op lucht- en watermassa’s.
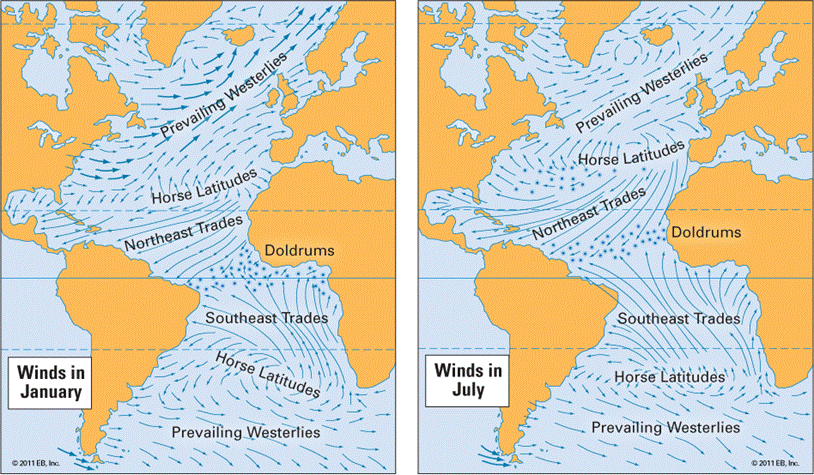
Dominante windrichtingen boven de Atlantische Oceaan in januari en juli. De eerder voorspelde zuidenwind wijkt dus af door het corioliseffect waardoor we in België vooral west- en zuidwestenwind krijgen. De dominante windrichting in de subtropen zowel in het noordelijk als zuidelijk halfrond noemt men passaatwinden (Trades). Bron: Britannica Encyclopedia.
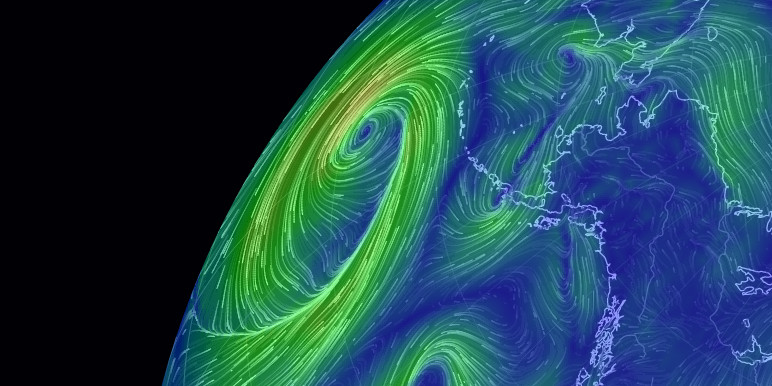
De werkelijkheid is alweer een stuk complexer dan wat hierboven wordt beschreven. Supercomputers kunnen ons vandaag een nog accurater beeld geven van de winden op aarde.
Klik op de figuur om een bewegende visualizatie van de wind te krijgen. Je kunt de wereldbol draaien. De data op deze wereldbol wordt iedere drie uur geupdated. Bron: Earth.nullschool.net